前一阵总结了一下常用的QR分解的方法，这里做一记录。

Gram-Schmidt正交化

基本思想

Gram-Schmidt正交化

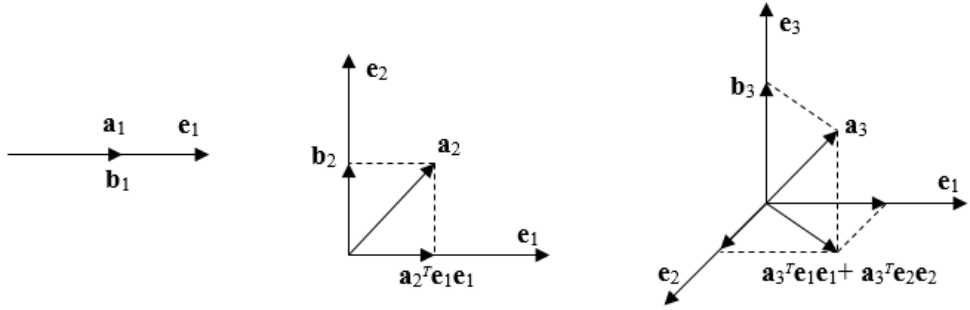
给定线性无关组$\alpha_1,\alpha_2,\cdots,\alpha_n$，构造单位正交基$q_1,q_2,\cdots,q_n$，使得$\text{span}(\alpha_1,\alpha_2,\cdots,\alpha_n)=\text{span}(q_1,q_2,\cdots,q_n)$。

采用的基本方法是投影法，即从$\alpha_1,\alpha_2,\cdots,\alpha_n$中依次减去其在$\text{span}(q_1,q_2,\cdots,q_{i-1})$上的投影，得到$q_i$。

$\alpha$在$\beta$上的投影是：$\frac{\alpha^T\beta}{\beta^T\beta}\beta$。

CGS算法

给定线性无关组$\alpha_1,\alpha_2,\cdots,\alpha_n$。

\[\begin{aligned} \widetilde{q_1} & = \alpha_1 \\ \widetilde{q_2} & = \alpha_2-\frac{\alpha_2^T\widetilde{q_1}}{\widetilde{q_1}^T\widetilde{q_1}}\widetilde{q_1} \\ \widetilde{q_3} & = \alpha_3-\frac{\alpha_3^T\widetilde{q_1}}{\widetilde{q_1}^T\widetilde{q_1}}\widetilde{q_1}-\frac{\alpha_3^T\widetilde{q_2}}{\widetilde{q_2}^T\widetilde{q_2}}\widetilde{q_2} \\ & \cdots \\ \widetilde{q_n} & = \alpha_n-\frac{\alpha_n^T\widetilde{q_1}}{\widetilde{q_1}^T\widetilde{q_1}}\widetilde{q_1}-\frac{\alpha_n^T\widetilde{q_2}}{\widetilde{q_2}^T\widetilde{q_2}}\widetilde{q_2}-\cdots-\frac{\alpha_n^T\widetilde{q_{n-1}}}{\widetilde{q_{n-1}}^T\widetilde{q_{n-1}}}\widetilde{q_{n-1}} \end{aligned}\]

得到的$\widetilde{q_1},\widetilde{q_2},\cdots,\widetilde{q_n}$是一组正交基。之后把每个向量单位化：$q_i=\frac{\widetilde{q_i}}{|\widetilde{q_i}|}$即可。

Classic Gram–Schmidt Orthogonalization算法 CGS

我们可以把上面的式子写成矩阵形式，对于可逆矩阵$A=\begin{bmatrix} \alpha_1 & \alpha_2 & \cdots & \alpha_n \end{bmatrix}$：

\[\begin{aligned} A & = \begin{bmatrix} \widetilde{q_1} & \widetilde{q_2} & \cdots & \widetilde{q_n} \end{bmatrix} \begin{bmatrix} 1 & -\frac{\alpha_2^T\widetilde{q_1}}{\widetilde{q}_1^T\widetilde{q_1}} & \cdots & -\frac{\alpha_n^T\widetilde{q_1}}{\widetilde{q}_1^T\widetilde{q_1}} \\ 0 & 1 & \cdots & -\frac{\alpha_n^T\widetilde{q_2}}{\widetilde{q}_2^T\widetilde{q_2}} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix} \\ & = \widetilde{Q} \widetilde{R} \\ & = Q \cdot diag(\|\widetilde{q_1}\|,\|\widetilde{q_2}\|,\cdots,\|\widetilde{q_n}\|) \widetilde{R} \\ & = QR \end{aligned}\]

仍能保证$R$是一个上三角阵，且对角元为$|\widetilde{q_1}|,|\widetilde{q_2}|,\cdots,|\widetilde{q_n}|$。

注：

  • $Q$是一个正交矩阵，即$Q^TQ=I$

  • $R$是一个对角元为正的上三角阵

  • $A$是满秩的方阵

  • 这样的分解是唯一的

事实上QR分解对非方阵$(m\times n,m \geq n)$也成立。

$m\times n$矩阵的QR分解

对于$m\times n$的矩阵$A$：

对于列满秩的矩阵$A$，第一条本身就是 Gram–Schmidt 正交化的结果，$Q_1$的列向量就是被正交归一化的$A$的列向量。

在此基础上，只用扩充$Q$的列向量，就可以得到第二条。

对$A$更新（补充）列的方法来证明第一条成立：

（奠基略去）如果结论对$m\times (n-1)$，考虑$A=\begin{bmatrix} A_0 & \alpha_n \end{bmatrix}$，其中$A_0=Q_1R_1$。

1.如果$a_n \in \mathcal{R}(Q_0)$，就可以找到一个$\mathbf{r}_n$，使得$\alpha_n=Q_0\mathbf{r}_n$，任取一个新的与$Q_0$列向量都正交的向量$\mathbf{q}_n$：

\[\begin{aligned} A & = \begin{bmatrix} A_0 & \alpha_n \end{bmatrix} \\ & = \begin{bmatrix} Q_0 R_0 & Q_0 \mathbf{r}_n \end{bmatrix} \\ & = \begin{bmatrix} Q_0 & q_n \end{bmatrix} \begin{bmatrix} R_0 & \mathbf{r}_n \\ \mathbf{0}^T & 0 \end{bmatrix} \\ & = Q_1 R_1 \end{aligned}\]

对$A$更新（补充）列的方法来证明第一条成立：

2.如果$a_n \notin \mathcal{R}(Q_0)$，我们直接做Gram-Schmidt正交化即可。

同之前地，$\widetilde{q}_n=\alpha_n - Q_0 \mathbf{r}_n$，$q_n=\frac{\widetilde{q}_n}{|\widetilde{q}_n|}$。

\[\begin{aligned} A & = \begin{bmatrix} A_0 & \alpha_n \end{bmatrix} \\ & = \begin{bmatrix} Q_0 R_0 & Q_0 \mathbf{r}_n + \|\widetilde{q}_n\| q_n \end{bmatrix} \\ & = \begin{bmatrix} Q_0 & q_n \end{bmatrix} \begin{bmatrix} R_0 & \mathbf{r}_n \\ \mathbf{0}^T & \|\widetilde{q}_n\| \end{bmatrix} \\ & = Q_1 R_1 \end{aligned}\]

这样就可以证明对于$m\times n$矩阵（不要求列满秩，若只使用GS正交化就只能为列满秩的矩阵）的QR分解。

复杂度及稳定性

复杂度、稳定性 下面计算这种方法的复杂度：

总的复杂度（约）为$2mn^2$ flops。

由于浮点数存储的舍入误差，在一定范围（误差积累）后，随着$n$增大，$Q$矩阵逐渐失去正交性，稳定性较低。

MGS算法

Modified Gram–Schmidt Orthogonalization 算法 MGS

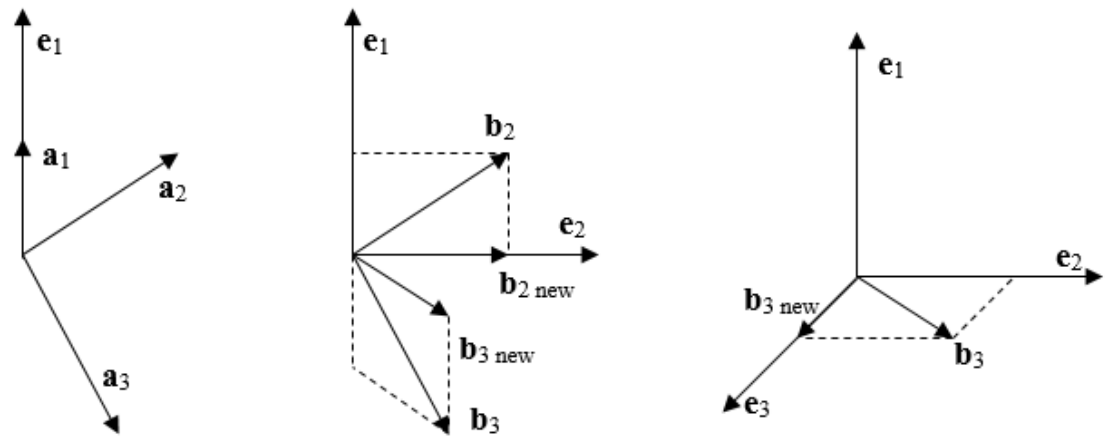
相当于对CGS改变了次序：

CGS每次计算$R$的一个列，MGS每次计算$R$的一行。

CGS不断增添$Q$的列，MGS不断把$A$调整为$Q$。

image image

CGS和MGS的对比

复杂度 CGM与MGS的过程是等价的，它们的复杂度相同，为$2mn^2$ flops。

稳定性 MGS的稳定性要比CGS高，它计算量越往后是逐步减少的，因此前面计算积累的误差的影响就不会剧烈地扩散开，所以MGS可以使求得的矩阵Q的正交性更好。

Householder与Givens变换

正交变换

正交矩阵

正交变换

二维的正交变换只有两种：旋转和反射。由此给出Householder变换和Givens变换。

Householder变换

Householder矩阵 $H_{\mathbf{u}}$是$\mathbb{R}^n$上的反射变换，反射面为$\mathbf{u}$的正交补空间：

\[\begin{aligned} H_{\mathbf{u}} & = I - 2\mathbf{u}\mathbf{u}^T \end{aligned}\]

其中$\mathbf{u}$是一个单位向量，$H$是一个正交、对称矩阵。

注意到对任意的$\mathbf{v}$，有：

\[\begin{aligned} \mathbf{v} & = (I-\mathbf{u}\mathbf{u}^T)\mathbf{v} + \mathbf{u}\mathbf{u}^T\mathbf{v} \\ H_{\mathbf{u}}\mathbf{v} & = (I-\mathbf{u}\mathbf{u}^T)\mathbf{v} - \mathbf{u}\mathbf{u}^T\mathbf{v} \end{aligned}\]

其中$(I-\mathbf{u}\mathbf{u}^T)\mathbf{v}$是$\mathbf{v}$在$\mathbf{u}$的正交补空间上的投影，$\mathbf{u}\mathbf{u}^T\mathbf{v}$是$\mathbf{v}$在$\mathbf{u}$上的投影。即$H_{\mathbf{u}}$把$\mathbf{v}$映射到$\mathbf{v}$在$\mathbf{u}$的正交补空间上的投影的负向量。

Householder变换

Givens变换

Givens矩阵 $G_{\theta;i,j}$是$\mathbb{R}^n$上的旋转变换，旋转面为$\mathbf{e}_i$和$\mathbf{e}_j$张成的平面：

\[\begin{aligned} G_{\theta;i,j} =\begin{bmatrix} \ddots & & \phantom{\cos \theta} & \phantom{1} & \phantom{1} & \phantom{1} & \phantom{-\sin \theta} & \phantom{1} & \phantom{1} \\ & 1 & \phantom{1} & \phantom{1} & \phantom{1} & \phantom{1} & \phantom{-\sin \theta} & \phantom{1} & \phantom{1} \\ \phantom{1} & & \cos \theta & \phantom{1} & \cdots & \phantom{1} & -\sin \theta & \phantom{1} & \phantom{1} \\ \phantom{1} & & \phantom{\cos \theta} & 1 & \phantom{1} & \phantom{1} & \phantom{-\sin \theta} & \phantom{1} & \phantom{1} \\ \phantom{1} & & \vdots & \phantom{1} & \ddots & \phantom{1} & \vdots & \phantom{1} & \phantom{1} \\ \phantom{1} & & \phantom{\cos \theta} & \phantom{1} & \phantom{1} & 1 & \phantom{-\sin \theta} & \phantom{1} & \phantom{1} \\ \phantom{1} & & \sin \theta & \phantom{1} & \cdots & \phantom{1} & \cos \theta & \phantom{1} & \phantom{1} \\ \phantom{1} & & \phantom{\cos \theta} & \phantom{1} & \phantom{1} & \phantom{1} & \phantom{-\sin \theta} & 1 & \phantom{1} \\ \phantom{1} & & \phantom{\cos \theta} & \phantom{1} & \phantom{1} & \phantom{1} & \phantom{-\sin \theta} & \phantom{1} & \ddots \\ \end{bmatrix} \end{aligned}\]

Givens变换

QR分解——Householder变换

利用Householer变换，我们也可以像上面一样通过地推(归纳)的方法来进行QR分解。对于$m\times n$的矩阵$A$：

1.$\alpha_1 \neq \mathbf{0}$：

我们可以构造一个Householder矩阵$Q_1$，使得$Q_1\alpha_n=|\alpha_n|\mathbf{e}_1$。从而$Q_1A$可以写成：

\[\begin{aligned} Q_1A & = \begin{bmatrix} \|\alpha_n\| & \mathbf{b}^T \\ \mathbf{0} & A_1 \end{bmatrix} = \widetilde{A}_1 \end{aligned}\]

而$A_1=Q_2\begin{bmatrix} R_2 \ O \end{bmatrix}$，从而：

\[\begin{aligned} \begin{bmatrix} 1 & \\ & Q_2^T \end{bmatrix} Q_1A & = \begin{bmatrix} \|\alpha_1\| & \mathbf{b}^T \\ \mathbf{0} & R_2 \\ \mathbf{0} & O \end{bmatrix} \end{aligned}\] \[\begin{aligned} Q^TA & =R \\ A & =QR \end{aligned}\]

2.$\alpha_1 = \alpha_2 = … = \alpha_j-i = \mathbf{0}$但$\alpha_j \neq \mathbf{0}$：

有$\begin{bmatrix} \alpha_j & \alpha_{j+1} & \cdots & \alpha_n \end{bmatrix}=QR_j$

从而$A=Q\begin{bmatrix} O & QR_j \end{bmatrix} = Q\begin{bmatrix} O & R_j \end{bmatrix} =QR$。

注

  • 这个证明也说明$n$阶正交阵可以表示成不多于$n$个Householder矩阵的乘积。

  • 在实际计算中，我们是对上式中的$A_1$继续进行Householder变换，使其第一列只有第一个分量。最后结果形如：

\[\begin{aligned} Q_{n-1}...Q_2Q_1A=\widetilde{A}_n \end{aligned}\]

Householder变换的复杂度与稳定性

复杂度 Householder变换QR分解的复杂度约$2mn^2-2n^3/3$ flops。

稳定性

QR分解——Givens变换

仿照用Householder变换进行QR分解的方法，利用Givens变换也可以对$m\times n$矩阵$A$QR分解。

注

  • 每次变换仅影响到第$j$行和第$k$行（$k>j$），所以不会影响到所有列的前$j-1$行元素。

  • 第$j$步关于第$j$和第$k$元素作Givens变换时，仅需对当前$A$的第$j, k$两行和第$j, j+1, \dots, m$列组成的两行的子矩阵作二维的Givens变换即可, 并且对第$j$列的两个元素的变换结果分别为$\sqrt{x_j^2 + x_k^2}$和$0$，不用重复计算。

如此进行$m$步后就把$A$变成了上三角形，共需要进行$mn - \frac12 n(n+1)$次Givens变换。

总结与比较

方法 复杂度 原理 稳定性
CGS $2mn^2$ 基于正交化定义 低
MGS $2mn^2$ 修正正交化过程 中
Householder $2mn^2-2n^3/3$ 基于正交变换 高
Givens $2mn^2(?)$ 基于正交变换 略低于Householder
方法 优点 缺陷
Gram-Schmidt 1.适合小矩阵计算;
2.可以随时停止计算		 1.不适合稀疏矩阵;
2.积累大量舍入误差;
3.必须保存整个矩阵，内存开销大
Householder 1.不显式计算Q;
2.最适合稠密矩阵		 1.无法中断;
2.对于稀疏矩阵会产生大量无效计算
Givens 1.最适合稀疏矩阵；
2.不会对零元素做无效操作		 1.无法中断;
2.不适合稠密矩阵计算，占空间大

参考